Final Report: Kingston Metropolitan Area Seismic Hazard Assessment
Chapter 3: Ground Motion Modeling for the Kingston Metropolitan Area

Figure 3.0 Wreckage and debris from the 1907 Kingston earthquake. In some places, the ruin was so complete that the streets were impassable (from Fuller, 1907).

3.0 Ground Motion Modeling in the Kingston Metropolitan Area

Wiggins-Grandison and Reid (1993) review the development of earthquake ground motion models for Jamaica and the Kingston Metropolitan area during the last 40 years. Instrumental earthquake data for the island of Jamaica during this period was judged by most investigators to be of insufficient quality to permit a direct assessment of earthquake risk using conventional Gutenberg-Richter frequency magnitude statistics or probabilistic seismic hazard assessment. Geologic data was also judged to be incomplete at the scales necessary to specify a seismic hazard assessment. There was a lack of evidence to identify individual faults as sources of earthquakes, since few if any observations of surface faulting were available. Global plate tectonic models developed during this era had large uncertainties on the scale of individual islands. Hence, the majority of probabilistic earthquake hazard models have been based on historic observations utilizing macroseismic data and intensity reports.

The first probabilistic ground motion models for the Kingston area were proposed by Shepherd (1971) and Shepherd and Aspinall (1980) using macroseismic data from the Tomblin and Robson (1977) catalog. Intensity observations in the Kingston area during the period 1880 to 1970 (see Figure 2.5) were converted to acceleration by Shepherd and Aspinall (1980) using the Gutenberg and Richter (1954) relationship,

Log a =I/3 -0.5

where a is the horizontal acceleration, in cm s^-2, corresponding to the Modified Mercalli Intensity I.

As seen in Figure 2.5, more than 20 damaging events (MMI > VI) were reported during the interval 1880-1960 for the Kingston area. This is the highest rate of reported activity on the island. Shepherd and Aspinall (1980) note that this rate is comparable to the numbers of events with MMI > VI in southern California during the interval 1915-1955 and suggest that Kingston in particular, and Jamaica in general, is comparable to the highest risk zone of the United States Uniform Building Code Classification.

Table 3.1 Estimates of return periods, probabilities and accelerations for earthquakes of Modified Mercalli Intensity VII or greater earthquakes in the Kingston area

Probability - probability of exceedence in 50 years
PGA - Peak Ground Acceleration based on intensity-acceleration relationships from 1.Gutenberg and Richter (1954), 2. Medvedev (1968)

For MMI IX level ground motions, Shepherd and Aspinall (1980) estimated an acceleration of 32% g with a 30% probability of exceedence in 50 years on hard rock (Table 3.1). Consideration of site amplification effects in the Liguanea Plain lead Shepherd and Aspinall (1980) to modify this estimate to 30% g with a 10% probability of exceedence in 50 years. This is the value that is currently used in the Jamaican Building Code.

A more recent regional seismic hazard assessment by Shepherd et al. (1997) for the Caribbean is based on a revised earthquake catalog with uniform seismic moment magnitude values. That study uses the Historic Parametric method to conduct a probabilistic seismic hazard assessment. As shown in Figure 3.1, their analysis of Jamaican seismicity indicates a Peak Ground Acceleration (PGA) high of approximately 30%g in eastern Jamaica and a gradual decrease to less than 14% g in western Jamaica for hard rock sites with a 10% probability of exceedence in 50 years. The values for the Kingston Metropolitan area are approximately 28% g.

One of the basic limitations of this type of analysis is that the period of completeness of historic or instrumental earthquake catalogs is very much shorter than the return periods of the earthquakes of greatest engineering and societal interest. The Pan American Institute of Geography and History (PAIGH) catalog (Shepherd et al., 1994) used by Shepherd et al. (1997) is complete for earthquakes of magnitude greater than 4 for the period 1964 to 1993. These data need to be extrapolated over 1 to 2 orders of magnitude, however, to estimate ground motion levels with 475-year return periods. This range of extrapolation also assumes stationary behavior. In other words, that the rates and locations of observed earthquake activity remain relatively constant over time periods longer than the catalog. Observations of decreasing seismic activity in Jamaica since the 1930's by Shepherd and Aspinall (1980) appear to indicate non-stationary behavior.

As discussed in Section 2, we have integrated all of the existing geologic and geodetic data for the region to develop, what we consider to be, a physically realistic earthquake hazard model for the Kingston Metropolitan area. This section of the Final Report contains:

• A description of the SEISRISK III ground motion modeling program used in this study.
• A discussion of regional earthquake ground motion attenuation models
• A presentation and discussion of the model results - these results are presented in terms of two levels of peak ground acceleration on hard rock as required for seismic design criteria.
  • Level 1 or moderate earthquake ground motions with a 50% probability of exceedence in 50 years, corresponding to earthquakes with repeat times of approximately 72 years. Level 1 ground motions correspond to levels of shaking that are likely to be experienced by a structure at least once during its lifetime. Also known as the Operating Level Earthquake, critical operations and facilities on made-ground in port and harbor areas should be designed to experience only minor non-structural damage.
  • Level 2 or severe earthquake ground motions with a 10% probability of exceedence in 50 years. Level 2 ground motions correspond to levels of shaking that have a more remote probability of occurrence during the life of a structure. This level of exposure corresponds to the exposure times specified for building design in the Caribbean Uniform Building Code (CUBiC) and other National Building codes. This level is also designated the Contingency Level Earthquake for many port and harbor facilities (Werner, 1998). Critical operations and facilities on artificial fill or made-ground in port and harbor areas should be designed to prevent major structural damage or collapse.
• A comparison of these results with previously published ground motion estimates.

These 'hard rock' ground motions will be combined with the geologic site classifications discussed in Section 4 to develop a composite ground motion map for the Kingston Metropolitan area.

Figure 3.1 Horizontal ground acceleration with a 10% probability of exceedence in 50 years (Shepherd et al., 1999). Contour interval is 25 gals (or 2.5%g)

3.1 Description of SEISRISKIII

The earthquake ground motion calculations and maps presented in the next section are based on the computer program SEISRISK III (Bender and Perkins, 1987). A brief description of the computational methods follows. Those wishing more detailed information about the program should refer to the original documentation. SEISRISK III is one of a series of computer programs developed by the US Geological Survey to calculate maximum ground motion levels that have a specified probability of not being exceeded during a fixed time period at each of a set of sites uniformly spaced on a two-dimensional grid. The earthquake sources are modeled as either points located randomly within seismically homogeneous source zones or as finite length ruptures that occur randomly along linear fault segments. In this study we examine both types of source zone configurations.

Figure 3.2 Distribution of earthquakes using source zone method. In A earthquakes only occur within well-defined seismically homogeneous source zones. In B, earthquakes locations are normally distributed with standard deviation s=10 km; in C, s= 25km; in D s = 50km.

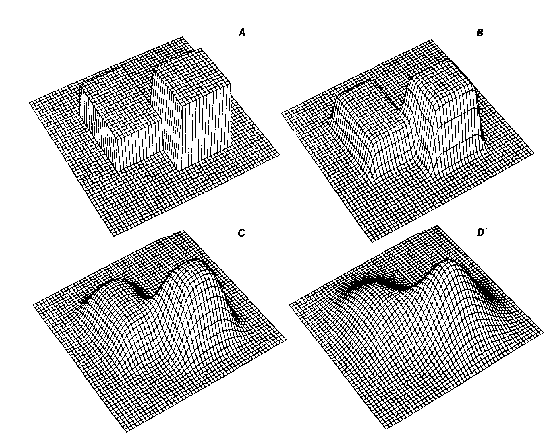
Typically, the precise edge of an earthquake source zone is usually ill defined. The SEISRISK III program permits the inclusion of earthquake location uncertainties to avoid abrupt changes in accelerations near source zone boundaries. Figure 3.2 from Bender and Perkins (1987) illustrates the effect of including source zone uncertainty on earthquake rates. Sources are modeled as normally distributed rather than uniformly distributed. We use this type of model for the Blue Mountains region, as well as a discrete fault model.

In certain cases, there is sufficient information to identify the active faults and determine the source properties of potential earthquakes. Faults are modeled as a series of straight-line segments. In reality, some fault segments will not touch, that is, there may be an identifiable discontinuity in the fault at the surface. Also, various fault segments may meet at greater or lesser angles sometimes indicating an abrupt change in the trend of the fault. Studies on the Anatolian Fault in Turkey (Kadinsky-Cade, 1988) suggest that fault segments with strike differences of more than 30^o will not rupture during one earthquake. In other words, these changes of strike act as barriers to earthquake ruptures. We therefore calculated maximum fault lengths by summing all of the segment lengths that had adjacent fault strikes differing by less than 30^o (Figure 3.3). We use this type of model for the Plantain Garden Fault zone, as well as the Rio Minho-Crawle River, and other simple, well-defined fault systems.

Figure 3.3 Fault consisting of three connected straight-line segments. A rupture may span several segments whose strikes differ by less than 30^o. Closest distance from rupture to site is used to determine ground motion at site.

For the purposes of this analysis, we assume that earthquake occurrence is Poissonian, which means

• that the number of earthquakes during any given time interval, Dt, is independent of the number of events prior to the beginning of the interval, and
• the probability of exactly one event in any interval of length Dt is proportional to the length of that interval with a constant l. l is the rate of earthquake occurrence or 1/ repeat time.

The probability of an event during a time interval, t, is given as

P(t) = 1 - e ^{- lt}

For fault specific models, fault rupture length, seismic moment and average displacement are based on empirical relationships developed by Wells and Coppersmith (1994) for strike slip faults:

Log (AD) = -1.70 (� 0.23) + 1.04 (� 0.13) log (SRL)

and

M = 7.04 (�0.05) + 0.89 (� 0.09) log (AD)

where AD is the average displacement in meters, SRL is the surface rupture length in km and M is the moment-magnitude.

Acceleration variability (s) takes into account variations in observed accelerations due to variability in the generation of accelerations at the earthquake source (earthquake to earthquake variability, fault-type, directivity of rupture, sub-events) as well as variations in path attenuation. Some authors recommend a s of 0.6 (Bender and Perkins, 1993) which represents a factor of 2 variation in ground motion from that calculated by the attenuation formula. Given uncertainties in acceleration decay curves (discussed in the next section) and variability observed in earthquakes worldwide, a variability of 0.6 is a good, conservative estimate (D. Perkins, personal communication, 1994). Lower values of variability result in an underestimate of expected accelerations.

Using the fault characteristics as given in Table 2.1, we developed a ground motion model for KMA. For each fault, a maximum earthquake size based on fault length was determined using the relations of Wells and Coppersmith (1994). As noted above we developed two distinct slip models, 151 and 511, to account for our uncertainty in the partitioning of slip throughout Jamaica. We were also left with an uncertainty in the magnitude-frequency relation (b-value) used to estimate the rate at which any given fault would produce events smaller than the maximum possible. Reasonable b-values for this tectonic environment range from 0.7 to 1.0. Each of these extreme values were used in conjunction with the 511 and 151 models to evaluate ground shaking. Another not well determined parameter, seismic wave attenuation, was also varied, using two models adopted by Shepherd et al (1997) for the Caribbean basin. We also used a seismic source zone instead of individual faults near KMA to see if there was any effect on the results.

When taking into consideration the two rates of input fault motion (6 and 8 mm/yr), two slip models (511 and 151), the use of discrete faults or source zones, as well as variations in b-value and attenuation laws, we found that a total of 32 different runs representing reasonable extremes in the input data were needed to model ground motion for the Kingston Metropolitan area. These variations in the ground motion model are summarized in the logic tree shown in Figure 3.4 for an input of 8 mm/yr.

Figure 3.4 Logic tree for the Kingston Seismic Hazard Assessment. Branches show variations to the input hazard model based on rates of fault slip for the Rio Mino-Crawl River and Duanvale faults (151 and 511), discrete faults or source zones as earthquake sources, b-value (0.7 and1.0) and attenuation laws (wc- Woodward-Clyde and jb - Joyner-Boore models) discussed in the text.

3.2 Attenuation Model

Once sources are identified, and the sizes and rates of activity estimated, one needs to account for attenuation of seismic waves from the source to the site to model ground motions. Phase One activities included the collection of isoseismal data for Jamaican earthquakes to evaluate the decay of Modified Mercalli Intensity (MMI) with distance. Wang et al. (1995) published an attenuation relationship for Jamaica using MMI as a function of distance,

MMI = 2.043 + 0.99 M_s -1.22 log (R) - 0.01R

where M_s is the surface wave magnitude and R is the distance from the epicenter to the site. MMI is a damage scale, however, and relates to ground accelerations in a complicated fashion. We need to know the actual attenuation of ground motion with distance in Jamaica as an input to the SEISRISK III ground motion model. With the exception of the February 26, 1978 earthquake, no strong motion recordings and no instrumental measurements of attenuation currently exist for Jamaica.

Several regional models have been suggested to bracket possible ground motion response in the Caribbean region and have been discussed by Tanner and Shepherd (1997) in their studies of Caribbean seismicity and ground motion. The Pan American Institute of Geography and History (PAIGH) has suggested using the Woodward-Clyde (1982) model for earthquakes with depths greater than 15 km throughout the Caribbean

ln A = 5.347 + 0.5 M -0.85 ln (D) + exp (0.463 M)

where A is the peak horizontal ground acceleration in gals, M is the magnitude and D is the distance from the source to the receiver. Shallow (<15 km) events in the Caribbean are modeled by using the Joyner and Boore (1993) relationship (The value 0.277 is misprinted in Shepherd et al. (1997) as 0.227.)

log A = -1.229 + 0.277 M -log (D² + 44.225)^� - 0.00231 (D² + 44.225)^�

This equation allows for increased acceleration for shallow focus earthquakes, however, the majority of data is from California earthquakes.

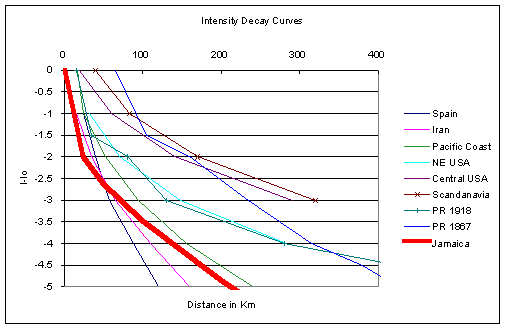
Comparison of these attenuation laws in Figure 3.4 indicates that the Woodward Clyde (1982) relation decays more slowly with distance than Joyner and Boore (1993) law and has a lower peak acceleration (30% of JB values) at short distances. Earthquake intensity data can provide a gross verification of regional attenuation relationships. Figure 3.5 compares the Wang et al. (1995) MMI decay curve for Jamaica with data from Puerto Rico and other regions with greatly varying intensity decays. The decay curve for Jamaica is in many ways similar to that of the Pacific Coast of the US; suggesting that the Joyner-Boore attenuation model, which is based on data from California, is more appropriate than that of Woodward-Clyde.

Figure 3.4 Comparison of ground motion attenuation laws used in this study. Note the very low rate of drop off of acceleration with distance for the Woodward and Clyde model.

Figure 3.5 Comparison of observed decay of Modified Mercalli Intensities with distance for various parts of the world. Note that the decay for Jamaica is similar to that observed for the Pacific Coast of the US. I-Io is the difference between the intensities for a specific earthquake. Io is highest intensity observed. Curve marked Jamaica is from Wang et al. (1995), other curves from Hayes (1987).

Efforts are currently underway to develop an empirical attenuation function for Jamaica using earthquake data from the new digital seismograph network described in Appendix 1 (Wiggins-Grandison, personal communication, 1999). Digital seismograms from recent earthquakes were analyzed to determine the coda-Q value for the entire island of Jamaica. The quality factor, Q, is a measure of the energy lost due to absorption and scattering as seismic waves propagate,

Q = Q_of^v

where f is the frequency and Q_o and v are constants.

Table 3.4 and Figure 3.6 compare preliminary Q values for Jamaica, with those from California and the Central United States. Both the MMI (Figure 3.5) and coda-Q (Figure 3.6) decay curves demonstrate that seismic attenuation in Jamaica is comparable to that observed in California.

Table 3.3 Comparison of coda-Q values

Figure 3.6 Comparison of coda-Q attenuation values for Jamaica, California, and the central United States.

3.3 Ground Motion Modeling Results

As noted above, 32 separate runs of the program SEISRISK III were needed to model a reasonable range of ground motions given the uncertainties in the input data. Figure 3.7 are the contour maps that we consider to be most reasonable for horizontal ground accelerations that are expected to not be exceeded at the 90% level within the next 50 years (or the10% probability of exceedence in 50 years). Firstly, it is apparent that use of the Woodward-Clyde attenuation model for subduction zones leads to excessively high-expected accelerations (0.50-0.85g) in the 50-year time frame. This is true regardless of the values of the other variables. Therefore, we concentrate on the results based on the Joyner-Boore attenuation model for shallow sources. This reduces the number of models from 32 to 16. The Joyner-Boore attenuation model seems more applicable based on the MMI (Figure 3.5) and coda-Q (Figure 3.6) decay curves and the fact that the majority of earthquakes in Jamaica are shallow and not due to the presence of a subduction zone.

Figure 3.7 475 year ground motion maps for various sources calculated using Joyner-Boore attenuation model for California. Right panels are calculated using source zone for Blue Mountain faults and probably underestimate accelerations (see text). Left panels are based on individual faults. The preferred combination of sources and attenuation are the left panels in Figure 3.7. These represent worst and best case models for the KMA.

Two types of ground motions patterns are seen in the remaining 4 strong motion maps (Figure 3.7). Those using faults to describe the strong motion threat to the KMA show a fairly uniform drop in accelerations from the NE to SW. The worst case model shows a range of accelerations throughout the Kingston Metropolitan area, varying from a high as 0.70g in the NE to a low of 0.35g in the SW. Maps based on the use of a source region to describe seismic sources in the Blue Mountain area show a similar range in accelerations, but with lower values in the SE, NE and N quadrants. We should point out that, despite the differences between the maps created using sources or faults for the Blue Mountains region, one general fact stands out- expected accelerations are significantly higher in the northeastern portion of the Kingston Metropolitan area than in the southwest.

The maps based on use of a source region in the Blue Mountains have the disadvantage of spreading out the region of possible seismic sources (see Figure 3.2), leading to 0.1g higher estimated accelerations in the western part of the Palisadoes, and the northernmost part of Kingston. These higher accelerations stem from the combination of events in the source region with events occurring on faults in the Yallahs Basin and the Crawle River fault respectively. Overall these maps show a decrease of accelerations along the length of the Blue Mountains. In our opinion, this result is not supported by the fault locations there. Therefore, we recommend use of maps 1517f8j and 5111f6j in Figure 3.7 for estimation of future ground accelerations on bedrock for the Kingston Metropolitan area. These two maps represent the worst and best case models for modeling active faults in the KMA. One should note that the difference between these two maps is about 25- 30 %g for the vast majority of KMA (see Figure 3.8). These variations primarily stem from the uncertainties in the amount of slip on the Crawle River Fault and the total amount of slip passing through Jamaica. Resolution of these two issues can dramatically reduce this uncertainty and improve strong ground motion estimates for the Kingston area.

Figure 3.8 Map showing difference in calculated acceleration between worst and best case preferred model for the KMA in Figure 3.7. Note that for the vast majority of the KMA, calculated accelerations vary by more than 25%g. The region of greatest variation is that closest to the Crawle River Fault system (NW corner of the map).

Figure 3.9 Calculated ground accelerations based on worst case model and no variation in acceleration due to uncertainties in source orientation and attenuation decay model (s = 0).

Figure 3.10 Map showing calculated ground accelerations using worst case model and 50% probability of non-exceedence in 50 years

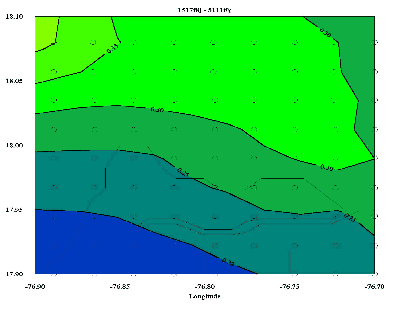
Figure3.9 shows ground motions according to the 'worst case' scenario with no variability in acceleration (i.e., s = 0) due to uncertainties in source orientation or attenuation decay. These values can be compared with other studies such as those of Shepherd and Aspinall (1980) and Shepherd et al. (1997). Finally, Figure 3.10 shows the worst case scenario with a 50% probability of exceedence in 50 years. This event was termed the Operating Level Earthquake, and represents the levels of ground motion that a facility could experience at least once during its operational lifetime.

It is worthy to note that previous investigators have found similar, but generally lower values for the Kingston Metropolitan area. Shepherd and Aspinall (1980) estimated values of about 30% g, and later Shepherd et al. (1999) again estimated values of about 28% g (see Figure 3.1) for a 10% probability of exceedence in 50 years. Both of these estimates were based on earthquake catalogs or intensity data (Historic Parametric method). While that record of strong earthquakes may be complete for the events of interest, it covers a time period that much shorter than the probable repeat times for most of the active faults. We feel that use of only the historic record will not give a complete picture of the actual earthquake threat. In the last 300 years, none of the important onland faults, capable of producing events in the magnitude 7.0 or larger range have moved. While the rates of motion and paleoseismic history of these faults have yet to be determined, we have already seen their potential importance in ground motion values for Kingston (Figure 3.7).

Table 3.4 Comparison of bedrock acceleration values (in %g) with a 10% probability of exceedence in 50 years

The peak ground accelerations shown in Table 3.4 range from 20 to 40 %g, and are comparable to ground motions estimated for Seattle, Washington (30 %g ); Portland Oregon (20 % g); Salt Lake City, Utah (30 % g) (Frankel et al., 1996) and San Juan, Puerto Rico (25% g) (McCann, 1994)