Caribbean Disaster
Mitigation Project
Implemented by the Organization of American States
Unit of Sustainable Development and Environment
for the USAID Office of Foreign Disaster Assistance and the Caribbean Regional Program
Caribbean Disaster
Mitigation Project |
Click here to view / print the complete set of figures for this document.
Preface
Executive Summary
1.0 Introduction
2.0 Hurricane Modeling and Predicted Windspeeds
3.0 Wind Loads and Response Estimates
4.0 Speed-Up Modification Factors
5.0 Geographic Distribution of Power Lines
6.0 Results
7.0 Summary and Recommendations for Future Work
8.0 References
Appendix A: Wind Loads and Response Estimates
Appendix B: Guyed Pole Analysis
This document was prepared as an activity of the Caribbean Disaster Mitigation Project (CDMP), a five-year regional effort being executed by the General Secretariat of the Organization of American States (OAS) with funding of the United States Agency for International Development. It reports the findings of a hurricane vulnerability and risk analysis of the electrical transmission and distribution system for St. Vincent. The study is part of a broader effort by the OAS and CARILEC, an association of Electrical Utilities in the Caribbean, to evaluate the vulnerability of the electric utility systems in the Caribbean to the impacts of natural hazards such as hurricanes and earthquakes.
This study was completed by Applied Research Associates of Raleigh, North Carolina. It consists of a comprehensive examination of the reliability and potential vulnerability of transmission and distribution systems to hurricanes in the Caribbean. The case study uses cost-benefit analysis and investment risk analysis to balance initial cost, operating cost and failure costs of the transmission and distribution system of St. Vincent's Electric Company (VINLEC) due to hurricane-produced wind failures.
The use of innovative wind engineering and stochastic modeling approaches in this study represents a significant step forward in understanding the risk of wind damage to electrical transmission and distribution systems in the Caribbean. Further work, however, remains to be done in the validation of the methodology, by expanding the number of case studies, and by a systematic analysis of system damages in future wind events.
Kirk P. Rodgers
Director
Unit for Sustainable
Development and Environment
Organization of American States
The study of the St. Vincent T&D system described herein is believed to be the first comprehensive study examining the reliability and potential vulnerability of electric power systems to hurricanes in the Caribbean. The approach used in the study uses the basic concepts of cost-benefit analysis and investment risk analysis that seek to balance initial cost, operating costs, and failure costs due to hurricane-produced wind failures. The methodology includes the following elements:
The results of the study can be used to determine the cost-benefits associated with new designs or upgrades of existing lines, to estimate the average annual dollar losses and the probabilities of losses exceeding specific dollar values (on a per year or per hurricane occurrence basis), and to address other insurance questions. The following paragraphs summarize key results of the study and recommendations.
Optimum Pole Size. In the numerical analysis, we simulated 10,000 tropical storms and hurricanes that pass within 250 kilometers of St. Vincent. The statistics of these simulated storms match those derived from historical records of all storms which have passed within 250 kilometers of the site during the period 1886-1994. As each simulated storm passes the Island, we compute the expected number of failed poles, examining the 33 kV line, the 11 kV lines and the low voltage lines separately. The replacement cost associated with the failure of the poles is computed using the cost information provided by VINLEC. Benefit-cost analyses were performed by replacing all the poles on the Island with larger, and more expensive (Class 1) poles and re-computing the failure costs for each of the 10,000 simulated storms.
Our analysis of different pole sizes provides estimates of the expected average annual losses, maximum losses, and number of failed poles for each pole type. The benefits produced by increasing the pole class are the reduction in the average annual losses (fewer failed poles) and the cost is the incremental cost associated with the difference in the cost of the existing class pole vs. an upgraded pole. The cost benefit analysis shows that it would have been more economic to build the 33 kV line using Class 1 Southern Yellow Pine poles, but upgraded versions of the 11 kV and low voltage lines would not have been economically justified.
Therefore, we recommend that if, during regular maintenance, poles along the 33 kV line need to be replaced, Class 1 poles should be used instead of the existing Class 3 poles. The remainder of the system appears to be adequately designed.
Expected System Losses. The expected financial losses are presented in terms of both average annual losses and losses vs. return period (or annual exceedance probabilities). This loss information can be used to help evaluate insurance needs. The expected average annual losses (replacement cost only) for the St. Vincent T&D system is in the range of EC $68,000 to EC $85,000. These values are shown in the following table along with other EC$ loss data. The average annual losses, including lost revenue (resulting from lost sales 4uring the period of line reconstruction) are estimated to be in the range of EC $110,000 to $134,000.
| Loss Cost Components | Average Annual Loss | Distribution of losses per Year1 | ||
| 50 yr. RP (0.02 EP) |
100 yr. RP (0.01 EP) |
500 yr. RP (0.002 EP) |
||
| Replacement Cost Only | 68-85 | 1,350 | 2,300 | 5,600 |
| Replacement & Lost Revenue | 110-134 | 2,000 | 3,900 | 9,200 |
1
50 yr. Return Period (RP) corresponds to a 2% annual Exceedance probability (EP)The mean replacement cost estimate of the 100 year return period loss (1% per year exceedance probability) is about EC $2.3 Million. Including lost revenue, the predicted distribution of losses for the 50, 100, and 500 year return period losses per year are EC $2, 3.9, and 9.2 million.
If the entire system were constructed using Class I poles the expected average replacement cost reduces to about EC $25,000 and the 100 year return period replacement loss reduces to about EC $0.8 Million. Therefore, although Class 1 poles are justified only for the 33 kV line, we see that if reduction in the probable maximum losses (PML) are important for insurability, then the use of Class I poles throughout St. Vincent would have reduced the 100 yr. PML from EC $2.3 to $0.8 Million. These types of loss data provide a rational basis for insurance and self-insurance decisions.
We note that the 100 year return period storm produces wind speeds on the Island corresponding to a storm producing medium category two wind speeds on the Island. The study includes information on the expected number of failed poles as a function of return period and as a function of the maximum peak gust wind speed occurring anywhere on the Island. We also note that the estimates of the fraction of failed poles given in the report expected as a function of the maximum peak gust wind speed anywhere on the Island will provide a means to further calibrate the model after future storms.
Validation and Sensitivity Analyses. The approach used in this study incorporates various models and data to quantify the losses to T&D systems in hurricane prone regions, and the technique provides decision support to assess the cost effectiveness of system design/upgrades and loss prediction. As indicated in the report, when assumptions need to be made regarding the vulnerability of the system, sensitivity studies are performed to ensure that decisions will not be significantly influenced by these assumptions.
Each of the models used has been tested and validated with data where possible. The windfield portion of the hurricane hazard modeling portion of the model has been extensively validated through comparisons to full scale measurements of hurricane wind speeds obtained from land falling hurricanes over the past two decades. The wind loading estimates are based on the state-of-the-art gust modeling techniques used to derive gust factors, etc. which are presented in wind loading provisions world wide. Information on the modulus of rupture of the wood poles is obtained from the results of full scale breakage tests performed in the United States. The individual components involved in the modeling process, including the hurricane model, the turbulence models, the gust factor modeling, have been validated through full scale testing and comparisons to full scale measurements. Calibration of the models in an end-to-end mode is needed to reduce some of the uncertainty in the predictions, particularly for the guyed-pole model developed explicitly for this study. However, as noted in the report, the sensitivity of the results to the guyed pole failure model did not influence the optimum pole size determination. We believe the approach used in the study represents the-state-of-the-art in the estimation of the failure of transmission systems subject to wind loads.
Sensitivity studies performed during the investigation examining the impact of topography and terrain show that both have a significant impact on the estimated number of failed poles, and because these features differ significantly between Islands in the Caribbean, the results obtained from this study should not be used to assess the vulnerability of systems on other islands. Other differences between St. Vincent and other Islands will include the effects of communication cables on the lines which are not common on St. Vincent but often exist on other Islands, as well as differences in span, pole type and hurricane wind climate.
Damage Surveys/Data. We believe that without analysis of the T & D failures that occur from Caribbean hurricanes and the incorporation of this information into the prediction methodology, that significant resources may be wasted in the Caribbean basin due to nonoptimum investments. There currently is no systematic plan in place to get even the most basic storm damage data, which is of immeasurable value in model validation and hence future loss mitigation. We believe the current methodology offers a solid basis for decision support, but it can and should be further validated and refined with real data.
We recommend that comparisons of predicted observed damage should be made for each utility in CARILEC that experiences hurricane damage. Detailed damage surveys should be performed to determine the total number of failed and tilted poles and the relative number of guyed pole failures and conductor or conductor connection failures. These failures should be mapped by pole location which would facilitate a recreation and simulation of the event for model evaluation. The damage surveys would require two engineers in the field for sufficient time to collect the detailed failure mode data which is needed to supplement the damage data obtained by the affected utility. This failure mode data would then be used in conjunction with a simulation of the storm to produce estimates of the wind speeds experienced by the structures during the event.
In addition, if good data exists for past storms, analyses and comparisons should be made; for example, gross comparisons of losses caused by Hurricane Luis on the Islands of Antigua and Anguilla, or the damage produced by Hurricane Marilyn in St. Thomas. Both of these storms occurred during 1995 and reasonably good information on the number of failed and tilted poles may be available. Note, that one advantage in using the Anguilla or Antigua data is that the islands are relatively flat and open and thus damage comparisons can be made without introducing significant terrain effects. This approach would allow the failure model to be tested without introducing additional uncertainties associated with the terrain model(s).
Need for Multi-Year Program. We believe that hurricane damage and significant economic impact to the Caribbean Basin remains a long term problem and that the development of cost-effective mitigation measure and estimation of loss potential are central to controlling both the losses and risks. Further, system vulnerability varies significantly from island to island and the optimum designs may differ as well. St. Vincent is known to have a "good" system and other islands are expected to be more vulnerable.
We recommend that a multi-year program be initiated to perform utility-by-utility assessments to investigate hurricane failures and collect critical damage data, for further validations, and to predict losses for individual utilities and all CARILEC utilities (considering multiple island strikes and multiple hurricanes in the same year). The investment by CARILEC in a multi-year program, including a task for damage data collection, would pay for itself many times over in improved decision making and optimum economic decisions.
The St. Vincent study identified a need for an improved method to analyze the failure probabilities for guyed structures and better information on the soil characteristics for use in foundation failure models. The study also indicates that improvements to the approach would be possible if more detailed information on the actual positions of pole/line type were available. This better data on pole position, etc. will eliminate the need to sample span lengths, line angles, etc., which add some uncertainty to the results.
The multiyear hurricane loss analysis and mitigation program would evaluate average annual losses and probable maximum losses for multiple island impact scenarios for the support of the development of an insurance pool. The potential payoffs resulting from a long term program include:
Without such a program, it will not be possible to estimate potential losses (average annual and PMLs) for the CARILEC utilities due to the complexities of multiple island strikes by the same event and multiple events per year over the Caribbean Basin.
Applied Research Associates (ARA) was retained by the Organization of American States (OAS) to perform a hurricane risk study for the electrical power Transmission and Distribution (T&D) system on the Island of St. Vincent, West Indies. The study includes the modeling of the hurricane hazard including the effects of wind direction, topographic and terrain effects on the hurricane wind speeds, wind load and response estimates of the T&D structures and the prediction of annual failure probabilities and annual failure costs associated with failure of the parts of the system in hurricane winds. The study includes the modeling of the entire transmission system on the island combined with an approximate modeling of the distribution system. Benefit-cost estimates are performed where the cost of upgrading portions of the system are compared to the future benefits expected as a result of fewer failures due to hurricane winds. In the benefit cost studies we examine the benefits associated with capital savings alone (cost of replacing the system with no consideration of lost income) and the benefits where the savings resulting from fewer lost sales of electricity are included.
Section 2 of this report discusses the hurricane hazard for St. Vincent and much of the Caribbean Basin results of the hurricane hazard simulation are compared to the Caribbean Uniform Building Code (CUBiC) values. Section 3 of the report discusses in detail the methodology used to estimate the response of the transmission and distribution system to wind loads, as well as discussing the methodology used to estimate the probability of failure given the occurrence of a wind speed. Section 4 of the report discusses the methods used to assess wind speed-up and Section 5 of the report discusses how the transmission and distribution system on the island is modeled. The integration of the hurricane hazard study, failure models, etc. is discussed in Section 6 along with the benefit cost results and a summary of the study.
Predictions of hurricane wind speeds on St. Vincent are obtained using the HURSIM hurricane simulation methodology described in Vickery and Twisdale (1 995a, 1 995b). Using this simulation approach, statistics describing the distance of closest approach (dmin), storm heading (q), translation speed (c), and central pressure (Dp) are derived for all storms which have passed within 250 kilometers of St. Vincent during the period 1886 through to 1994. The size of the storm, as defined by the radius to maximum winds (Rmax) is described using the model given in Vickery and Twisdale (1995b), which reproduces the observation that the more intense storms are generally characterized by small radii than the weaker storms. Tracks of the 102 storms which have passed within 250 kilometers of St. Vincent are given in Figure 2.1 where it is readily seen that storms affecting St. Vincent travel in an east to west direction. Using the statistical distributions of central pressure, etc., simulations of hurricane wind speeds at the site are obtained by randomly sampling from the derived statistical distributions of heading, central pressure, translation speed and distance of closest approach. Using the sampled storm properties, the hurricane wind field model is then used to simulate hurricane wind speeds. The simulated hurricane is passed through the simulation region along a straight line path with the modeled wind speeds and directions recorded on an hour by hour basis at as many points within the region that are of interest. A total of 10,000 simulated storms are used in the study. The overall simulation methodology is shown schematically in Figure 2.2. The wind speeds produced by the simulation methodology correspond to one hour average values in flat open terrain or coastal locations. Wind speeds corresponding to other averaging times or terrain conditions are derived as needed.
Once the 10000 storms have been simulated, the probability that the hurricane wind speed is exceeded during the time period, t, is
Equation 2.1
where P(v>V|x) is the probability of exceeding the velocity, V, given the occurrence of x storms, and pt(x) is the probability of x storms occurring during the period t. Assuming a Poisson process for pt(x), and defining the time period, t, as one year, equation (14) can be simplified and re-arranged in the form:
Equation 2.2
R = 1/[1.0-exp(lP(v>V))]
where l is the mean number of storms per year passing within 250 kilometers of the site (0.963), and R, is the return period associated with exceeding the wind speed, n. The probability of exceeding the specified wind speed, n, is computed from
Equation 2.3
P(v>V)=1-i/(N+1)
where i is the rank position of velocity n, within the N (10000) wind speeds obtained from the simulated storms.
Single point predictions of hurricane wind speeds were performed for 10 islands (Puerto Rico south to Grenada) with the results compared to the wind speeds given in the Caribbean Uniform Building Code (CUBiC) for return periods of 50 and 100 years. The mean hourly wind speeds resulting form the HURSIM simulations are adjusted to 10 minute values for comparison to the values given in the CUBiC code. Comparisons are given in Figure 2.3. As indicated in Figure 2.3, the HURSIM wind speeds are slightly lower than those given in the CUBic code. This result is expected as the wind field model used to develop the CUBiC code uses a conservative ratio of the value the surface level wind speeds to the gradient level wind speeds. All windspeeds are representative of open country or coastal values at a height of 10 m above ground.
Figure 2.4 shows the mean hourly wind speed at surface level plotted vs. return period for St. Vincent as well as the directional characteristics of the hurricane wind speeds. As indicated in Figure 2.4 the hurricane wind speeds have a strong westerly bias. Figure 2.5 shows the predicted hurricane wind speeds plotted vs. return period for averaging times of one hour, 10 minutes, one minute and 3 seconds. Also shown in Figure 2.5 are the 50 year return period wind speeds as specified in ASCE 7-95 for two locations in Florida, USA, where in is readily seen that the 50 year return period wind speed at St. Vincent is significantly lower than the two Florida locations given in Figure 2.4.
Also shown in Figure 2.4 are the return periods associated with a point location on the island experiencing wind speeds corresponding to Category 1 storms, Category 2 storms, etc. Note that the wind speeds experienced at a site are not necessarily associated with the maximum wind speeds within the storm, and thus, for example, a Category 5 storm passing to the north of the island may produce maximum winds on the island of only Category 1.
For use in the estimation of damage to the transmission and distribution system on the island, simulated hurricane wind speeds and directions are obtained at the center of 350 squares 0.01� by 0.01�.
The methodology used to estimate the wind loads acting on the transmission and distribution systems is based on the approach discussed in Davenport (1979). The methodology takes into account the variation of wind speed with height, the lack of correlation of the wind gusts and the effects of surface roughness and wind direction. Details of the wind loading methodology are given in Appendix A. The structure of the wind near the ground used in the wind loading portion of the model is based on the Engineering Sciences Data Unit (ESDU) models developed in the United Kingdom. These turbulence models are derived using a combination of theoretical models and full scale observations and are believed to be the best models available for estimating the characteristics of the near ground flow field. Details of the near ground wind modeling are given in Appendix A.
Each section of the distribution system is modeled assuming the pole acts as a simple cantilever fixed at a depth of 1 foot below grade. The conductors are modeled using half the span extending in each direction from the pole. The influence coefficients associated with the base bending moments are the height above ground plus 1 foot for loads acting on the pole, and the attachment height plus two feet for the conductors, ground wire(s) and communication wires. To compute the bending moment distribution and deflected shape, the pole is descritized into N sections each having a length of 1.0 feet. Each section is assigned a height, diameter, mass, drag coefficient, and flexural rigidity, El. Each conductor, ground wire and communication cable is divided into 100 segments, with each section assigned a height, z a lateral co-ordinate, y. The diameter and drag coefficient of the conductor is held constant across the span. In instances where poles support transformers an additional point wind load is allowed for by increasing the value of the drag coefficient times the projected area (CdA) at the height corresponding to the center of the transformer.
Influence coefficients describing the deflected shape of the pole are developed to account for the contributions of the distributed wind load acting over the height of the pole and the point loads acting at the connection between the pole and the conductors, accounting for the effect of wind loads acting on the conductors. Using the approach given in Appendix A, the peak bending moment one foot below grade is computed as a function of the peak gust wind speed at a height of 10 meters above ground. For each wind speed examined, the deflected shape of the pole is obtained and additional deflections and moments due to self weight of the pole, conductors and transformers (if needed) (i.e. P - D) are computed and added to the moments and deflections due to wind action alone. Pole geometry information is derived from the ANSI tables providing information on pole circumference at one foot intervals along the length of ANSI standard wood transmission and distribution poles. The Tables used in this study were provided by Florida Power and Light (FPL). Peak base bending moments are computed for peak gust wind speeds ranging between 37 mph to in excess of 500 mph in increments of 15 mph. This peak base moment vs. wind speed information is then used to develop failure probability distributions as described below.
A pole is considered to have failed if the bending stresses one foot below the ground line exceed to modulus of rupture of the wood pole. The statistics (mean and standard deviation) of the modulus of rupture were taken from Goodman and Stewart (1990). The strength data given in Stewart and Goodman (1990) present observations of failure stresses m Southern Yellow Pine poles covering a range of ages varying from new to m excess of 50 years old. In the case of new poles the mean value and coefficient of variation of the modulus of rupture, based on ANSI specified pole dimensions were found to be 8490 psi and 0.192, respectively. In the case of twelve year old poles the mean value and coefficient of variation of the modulus of rupture based on ANSI dimensions were found to be equal to 5185 psi and 0.267 respectively. To enable modeling of the reduction in strength with age, the modulus of rupture, sr and associated coefficient of variation, COV, are modeled as
Equation 3.1
sr = 8490exp(-0.0411T)
COV = 0.192exp(0.134T)
where T is the length of time the pole has been in service. Figure 3.1 shows the modulus of rupture at ground line (MORGL) vs age for utility poles sampled in the United States, where it is seen that alter a period of time of about 10 to 12 years the reduction in pole capacity with time appears to cease. Also shown in Figure 3.1 (solid line) is the Equation 3.1 (converted from AMORGL to MORGL) for service ages of up to 10 years.
In order to estimate failure probabilities as a function of wind speed. simulations were performed where the failure stress is sampled from a log-normal distribution with a mean and coefficient of variation defined as in Equation 3.1 The peak wind induced bending moment, one foot below ground line as a function of the peak gust wind speed at 10m is computed using the methodology outlined in Appendix A. An error term having a mean value of one and a coefficient of variation of 0.2 is used to multiply the computed wind load effect. The error term is takes into account uncertainties associated with the peak factor, g, the drag coefficients, the length scale parameters, the assumed surface roughness and the response calculations. The single pole failure probability distribution is obtained by sampling a modulus of rupture and a wind load uncertainty factor and then increasing the peak gust wind speed until the computed bending stress one foot below grade exceeds the sampled modulus of rupture. In each case examined, 5000 simulations are performed to develop the failure probability distribution. The failure probability distributions are developed for a spans ranging between a minimum of 50 feet and a maximum of 650 feet, in increments of 50 feet, for a range of speed up factors, and conductor and transformer combinations.
The transmission/distribution system on St. Vincent is comprised of a 33 kV transmission line, an 11 kV transmission line which is often underbuilt with low voltage lines, and a low voltage distribution system. The 11 kV line consists of both a single phase line (two conductors) and a three phase line (4 conductors). The underbuilt portion of the 11 kV line is either a single phase line (2 low voltage conductors) or a three phase line (4 low voltage conductors). In some cases communication cables are also carried along the same poles, but this is relatively uncommon and Cable and Wireless is in the process of putting all communication cables underground. Table 3.1 shows the type and number of conductors used in the various applications described above. In cases where more than one conductor type appears in one row in Table 3.1, either one of the conductor types may be used. Table 3.2 provides information on the conductor weights and diameters for use in the wind load calculations.
| Application | Conductor Type | |||
| 150AL | 100AL | 50AL | 50ACSR | |
| 33 kV Transmission | 3 | |||
| 11 kV Transmission (3 Phase) | 3 | 3 | ||
| 11 kV Transmission (1 Phase) | 2 | |||
| 400 V Low Voltage Distribution | 4 | 4 | ||
| 230 V Low Voltage Distribution | 2 | 2 | ||
| 400 V Low Voltage Distribution (Underbuilt) | 4 | 4 | ||
| 230 V Low Voltage Distribution (Underbuilt) | 2 | 2 | ||
The effects of wind speed-up due to the topography of the island must be considered in the simulation. Optimally, estimation of these effects would use a scale model wind tunnel study of the island or a three dimensional CFD simulation. These approaches are not feasible within the budget of the present study. Instead, speed-up modification values are estimated using a numerical model of the island topography combined with an empirical model for speed-up over hills.
A three-dimensional numerical model of the island is first developed by digitizing several hundred point elevations obtained from contour maps. A topographic surface representation of the island is then developed by interpolating surface elevations over a fine grid covering the island and surrounding sea surface. The elevation information was originally obtained using the Digital Chart of the World data base, however, the elevation information was too course and thus elevation information was primarily based on the 1:25000 map provided by VINLEC. Minimum curvature spline interpolations are used to define the surface between the digitized point elevations. The resulting model of St. Vincent island is shown in Figure 4.1
A two-dimensional model of elevation along the wind path is then established for each point of interest and for each wind direction. At each point of interest, a wind corridor approximately 3/4 km wide is considered and the variation of elevation is traced out upwind and downwind from the point of interest. The elevation is averaged across the width of the corridor. In order to assure that a reasonable fetch has been considered, the elevation is traced out in each direction until it drops to at least one half of that at the point of interest. This results in a cross-section of elevation such as shown in Figure 4.2.
The cross-section is then approximated by a two-dimensional escarpment defined by two parameters: the maximum height, H, and the horizontal distance to half height, L. A simple speed-up model put forth by Lemelin [1987], is then used to derive a speed-up ratios as follows,
Equation 4.1
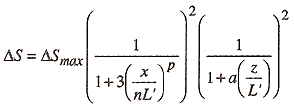
Equation 4.2
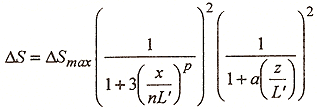
where x is the horizontal distance from crest of the hill to the point of interest positive if on the leeward side), and z is the height above the surface at the point of interest. The remaining parameters have been determined empirically and take on the values shown in Table 4.1.
On the leeward side of the hill, the model assumes the point of interest is on the top of the escarpment and the speed-up will be conservative.
This simple model does not provide appropriate speed-up factors in every instance. It is very easy to imagine cases where the escarpment described by the H and L values is quite different than the actual cross section. Also the topographic variations in the across wind directions may have significant effects in some cases. The approach does, however, give reasonable estimates in lieu of more elaborate analyses or physical model testing, neither of which could be carried out for the present study.
This simple escarpment model is applied every 0.5 km for a grid of points covering the island and for each of 16 wind directions around the azimuth. Figure 4.3 shows a qualitative map of speed-up ratios for a wind coming from the east. The complete set of such maps showing speed-ups for each of the 16 wind directions are given in Figures 4.4 through 4.19.
| DSmax | L' | a | n | p | ||
| H/L < 1 | 1.3 x H/L | L | 2 | x < 0 x > 0 |
1 5 |
2 1 |
| H/L > 1 | 1.3 | H | 0.6 | x < 0 x > 0 |
0.5 10 |
2 1 |
An important feature of the transmission/distribution system modeling procedure is obtaining a reasonably accurate estimate of the location of each pole on the Island. The information available form VINLEC does not allow for the precise positioning of every pole on the island and thus approximate methods are used. In this investigation a probabilistic model is used to ascertain the span length distributions and pole position information for each of the transmission and power distribution systems.
The probabilistic models adopted, are based on span lengths measured from detailed drawings of the layout of power lines for several different regions of St.-Vincent. In each case, the regions are representative of the transmission and power distribution systems throughout St.-Vincent. Using the drawings supplied by VINLEC samples of span length and line angle were obtained by hand. The resulting database of span lengths and line angles provides a sufficient sample space on which to fit probabilistic models of span lengths or line angles. Figures 5.1 through 5.3 show lognormal fits to the sampled span lengths for the 11 kV line, the 33 kV line and the low voltage lines. As indicated in Figures 5.1 through 5.3, the number of data points extracted for the 11 kV line, the 33 kV line and the low voltage lines are 471, 38, and 736 sample spans, respectively. In each case the log-normal distribution provides a reasonable fit to the span length data.
In the present study, high voltage transmission lines are approximated by a series of connected straight line segments. Line segments for the entire 11 kV (red) and 33 kV (cyan) high voltage transmission systems are shown in Figure 5.4. The start and end of each line segment is assigned a latitude and longitude. The start and end coordinates of each line were obtained by remapping the information given on the small scale maps and map segments provided by VINLEC onto a large 1:25000 scale map of the island.
The plotted 11 kV line segments have a total length of approximately 100 miles versus an actual length of approximately 190 miles. In many areas of St.-Vincent, the 11 kV line follows roads which tend to meander rather than be constructed in the straight line segments as depicted in Figure 5.4. This following of the winding roads is thought to account for the discrepancy between the actual and plotted length of 11 kV line. Figure 5.5 is a schematic diagram depicting this discrepancy. As is clearly seen, a straight line approximation may not always capture the true length of the line, resulting in a significant reduction of the total length of plotted line. In this particular example, the ratio of actual line length to straight line approximation is ~ 1.7.
The length discrepancy found for the 11 kV line is taken into account by applying a length factor, Lf =1.9, to each of the 11 kV line segments shown in Figure 5.5. This ensures that the proper amount of lines and poles are distributed throughout the island. Noting that the projected distance from the actual pole location to the straight line approximation (see Figure 5.5) is much less than the grid resolution used to compute hurricane wind speeds and wind speedup factors, application of a length factor does not affect the wind conditions that a utility pole would otherwise experience.
The total length of plotted 33 kV line is approximately 13 miles versus the actual 12 miles. Agreement between the plotted 33 kV line and the actual total length is not surprising since most of this line passes straight through undeveloped bush areas. In this case, a length factor Lf =1.0 is used. Leaving the 33 kV line segments unaltered results in a conservative overestimate of the total number of 33 kV utility poles.
A portion of the St. -Vincent west coast is shown in Figure 5.6, where it can be seen that a pair of latitude and longitude coordinates are assigned for each of the factored transmission line segments. Using these coordinates the length of the segment is computed and an appropriate number of spans is sampled from the lognormal distributions, previously shown in Figures 5.1 and 5.2 for the 11 kV and 33 kV lines, respectively. Sampling continues until the total length of spans is representative of the factored segment length. Once the number and length of spans is known, a specific set of coordinates is allocated to each utility pole (given the symbol � ) within the segment. The utility pole coordinates are then used to "look up" tabulated hurricane wind speeds, directions and wind speedup factors.
Power line span orientations are determined by adding to the line segment direction an angle correction factor, Dq. The angle correction factor is sampled from a lognormal distribution, shown in Figure 5.7. The probabilistic model is based on line angles measured from the same detailed drawings as are power line spans. In order to achieve a lognormal fit, the span orientation database was truncated at Dq =0�.
In the present study a value of x is sampled from a uniform distribution between 0 and 1. If the angle correction factor is automatically assigned Dq =0� otherwise the lognormal distribution is used to define Dq. The limiting value of x is determined from measured occurrences of Dq=0�, i.e., 57% of the measured span orientations were 0�. The rationale behind sampling span orientations reflects the tendency of the 11 kV lines to follow meandering coastal roads where changes in the line direction are quite frequent. In the angle sampling procedure, the sign of the angle, Dq, alternates from sample to sample, so that the net angle change between two well separated points is zero. Span orientations for the 33 kY line are assumed to be the same as the line segment directions since the large majority of these transmission lines actually follow the line segments.
Span lengths for the low voltage power distribution systems are obtained in a manner similar to transmission spans, i.e., they are sampled from the lognormal distribution, previously shown in Figure 5.3. The number of straight line segments required to define the low voltage distribution system approaches the actual number of individual spans, rendering application of the straight line approximation method impractical. Consequently, an alternate method is adopted for determining individual pole locations.
The method is based on the notion that a region being supplied power can be defined by several subregions. Each subregion is chosen to represent a small area of a specific region of power distribution. The area of each subregion is < 0.5 km2. The upper limit placed on the size of an area reflects the choice of grid size used to compute hurricane wind speeds and wind speedup factors. Since the area of each subregion is relatively small, the actual shape is not of consequence. A total of 208 power distribution subregions are defined to represent the total surface area of 139 power distribution regions. Information concerning the power distribution regions is provided by VINLEC. Figure 5.8 shows the location of all 208 subregions, represented by the symbol ' + '. Together they total the regions of power distribution for the whole of St.-Vincent. Combining regional utility pole density information made available by VINLEC, an appropriate number of spans/poles is assigned to each of the 208 distribution subregions. Hurricane wind speeds and speed-up factors are assigned to each subregion based on its central coordinates. All utility poles falling within a defined power distribution subregion are assigned the same wind conditions. Power line orientations are assigned by sampling from a uniform distribution.
Table 5.1 provides a summary of the number of poles and total length of power lines used in conjunction with the hurricane simulations.
| Line Type | 33 kV Line | 11 kV Line | LV Line |
| Simulated Number Poles | 251 | 7,371 | 8,958 |
| Simulated Length (miles) | 13.7 | 192.9 | 230.8 |
Using the information on wind speed-ups.. pole-span position and direction data, and wind speed and direction data described in the previous Sections, estimates of the expected number of failed poles per storm are derived. At each pole location, and for each simulated storm, the mean failure probability, is computed from
Equation 6.1
where ![]() is the mean failure probability of the pole for winds
approaching from direction, j. The probability of failure for winds approaching
from direction, j,
is the mean failure probability of the pole for winds
approaching from direction, j. The probability of failure for winds approaching
from direction, j, ![]() , is given as
, is given as
Equation 6.2
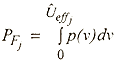
The failure wind speed probability density function, p(v), is obtained from one or more
of the log-normal failure wind speed distributions described in Section 3 and is a
function of the wind speed-up factor, span length and surface roughness, and ![]() is the effective peak gust wind speed in flat terrain, defined as
is the effective peak gust wind speed in flat terrain, defined as
Equation 6.3
where ![]() is the maximum peak gust speed approaching from direction j
produced by the simulated storm, and qj is the angle
between the direction normal to the direction of the line and the wind direction vector.
Note that the use of Equations 6.1 through 6.3 yields the failure probability associated
with the largest load effect seen over the sixteen wind directions. The parameters
defining the log-normal distribution (logarithmic mean and logarithmic standard deviation)
are obtained by linearly interpolating between the results for span lengths and speed-up
factors above and below the values of interest. This interpolation is performed separately
for both the open country exposure case and the suburban exposure case, yielding two
failure probability distributions for each of the sixteen directions. The "true"
wind speed at the site is obtained through the use of the ESDU roughness length transition
model. Using this model, the effective peak wind speed at the site is computed taking into
account the length of suburban fetch. The terrain is considered to be fully suburban for
any fetch greater than or equal to 20 kilometers. Any location within one kilometer from
the coast is considered to be in open terrain. Note that in a fully suburban terrain, the
mean wind speed at a height of 10 meters above ground has a magnitude equal to 71% of the
open country mean wind speed, and the peak wind speed at the 10 meter height has a
magnitude equal to 85% of the open country value.
is the maximum peak gust speed approaching from direction j
produced by the simulated storm, and qj is the angle
between the direction normal to the direction of the line and the wind direction vector.
Note that the use of Equations 6.1 through 6.3 yields the failure probability associated
with the largest load effect seen over the sixteen wind directions. The parameters
defining the log-normal distribution (logarithmic mean and logarithmic standard deviation)
are obtained by linearly interpolating between the results for span lengths and speed-up
factors above and below the values of interest. This interpolation is performed separately
for both the open country exposure case and the suburban exposure case, yielding two
failure probability distributions for each of the sixteen directions. The "true"
wind speed at the site is obtained through the use of the ESDU roughness length transition
model. Using this model, the effective peak wind speed at the site is computed taking into
account the length of suburban fetch. The terrain is considered to be fully suburban for
any fetch greater than or equal to 20 kilometers. Any location within one kilometer from
the coast is considered to be in open terrain. Note that in a fully suburban terrain, the
mean wind speed at a height of 10 meters above ground has a magnitude equal to 71% of the
open country mean wind speed, and the peak wind speed at the 10 meter height has a
magnitude equal to 85% of the open country value.
The logarithmic mean, mln v and standard deviation, sln v, of the failure wind speed are computed from
Equation 6.4a
and
Equation 6.4b
where the transition parameter, r, is defined as
Equation 6.5
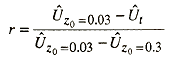
�t is the peak gust wind speed in the transition region and �z0=0.03 and �z0=0.03 are the peak gust wind speeds in homogeneous open terrain and suburban terrain's respectively. The transition parameter, r takes on a value of 0 for open terrain conditions and 1 for suburban terrain conditions. Once the logarithmic mean and standard deviations are computed for each direction, the integral in Equation 6.2 is evaluated using the approximation given in Abramowitz and Stegun (1970), and the pole failure probability is finally computed using Equation 6.1. The methodology described above is summarized in Figure 6.1. The expected number, E(n), of failed poles per storm is given as
Equation 6.6
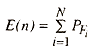
where ![]() is the probability of failure of the ith
pole, and N is the total number of poles. The expected cost of failure,
is the probability of failure of the ith
pole, and N is the total number of poles. The expected cost of failure, ![]() is given as
is given as
Equation 6.7
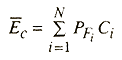
where Ci is the cost of failure of pole I.
For each failure probability computation, the pole position and the span orientation and span length are defined as was discussed in Section 5, but in the case of the 11 kV lines and the low voltage lines, information on the exact line type is not known. In the case of the 11 kV line, 73.44% of the line is 3 phase, with the remainder being single phase. Of the total 11kV line length, 5.7% of the line has 3 phase low voltage under built lines, 66% is under built with a single phase low voltage line and 28.3% carries no low voltage lines. In the case of the low voltage line, 4.4% is 3 phase with the remainder being single phase. During the simulation process the line type associated with each pole is obtained by sampling a random number from a uniform distribution (uniform between zero and one) and assigning a line type according to the proportions noted above. In the case of the 11 kV line, 15% of the lines with a single phase under-built low voltage line are assumed to be fitted with transformers.
The failure probabilities are representative of the mean (or expected) value per storm. Estimates of the variance of these failure probabilities is beyond the scope of work for this study.
Note that in the computation of failure probabilities, failure costs, etc. presented here, we use the simulated hurricanes resulting from the methodology outlined in Section 2 of this report. We were supplied with wind speeds over the island resulting from the simulation of a weak class 4 hurricane provided by Mr. Charles Watson. The results of this simulation could not be used in the study because:
Cost Model. The cost components included in the study here do not include maintenance costs since they are not explicitly known. The omission of maintenance does not impact the benefit-cost analysis since wood poles are used throughout and thus the maintenance costs are the same for all design options considered. The cost model used considers initial cost, replacement costs and an estimate of lost revenue.
The expected lifetime cost of the system including initial costs and failure costs, assuming a Poisson arrival process for the storms is given as
where C1 equals the initial cost; ![]() is the mean
failure cost per event; T is the assumed useful lifetime of the system; i is
the effective discount rate; and l is the average annual
occurrence rate of the storms.
is the mean
failure cost per event; T is the assumed useful lifetime of the system; i is
the effective discount rate; and l is the average annual
occurrence rate of the storms.
The cost of replacing a failed pole is assumed to be the same as the original installation cost and we assume that the conductors can be salvaged in all cases. Cost information was supplied by VINLEC for the class 3 pole 11 kV system and the class 5 pole low voltage system. In the estimates of the costs to replace failed poles used in the 33 kV line we assume that the material costs are the same as for the 11 kV line, but the petty contractor cost is doubled and the total man hour estimate is increased to 100 hours per pole instead of the 28 hours used for the 11 kV pole installation. Estimates of costs to upgrade the system to Class 1 poles throughout were estimated using pole cost data supplied by the General Wood Preserving Company (GWPC), in Leland, North Carolina. Table 6.1 presents the cost of the poles as supplied by GWPC for poles treated with 0.6 CCA.
| Pole Class | Cost ($US) | |
| 35 Foot Southern Yellow Pine | 45 Foot Southern Yellow Pine | |
| 1 | 197.70 | 304.90 |
| 2 | 172.30 | 264.80 |
| 3 | 149.10 | 235.30 |
| 4 | 136.80 | 204.50 |
| 5 | 114.70 | 171.00 |
| 6 | 98.30 | |
To estimate the increase in cost associated with upgrading poles, we increased the cost of the poles as supplied by VINLEC by the ratio of the pole cost as supplied by GWPC. For example, the cost of a 45 foot Class 3 pole in St. Vincent is $839.17 EC, and the estimated cost of a 45 foot Class 1 pole is 839.17(304.90/235.30)=1087.38 $EC. With this assumption, the cost of a 45 foot Class 1, unguyed G construction pole is 2018.64 $EC vs. the 1690.89 $EC for the Class 3 pole, an increase of 19%. Table 6.2 presents the replacement costs of the poles used in the study.
In Table 6.2, the cost of the 11 kV poles represents an estimate of the cost of the poles, taking into account that the construction type varies (i.e. G type construction, H type construction, etc.). For the Low voltage poles, only the guyed pole cost was supplied by VINLEC. To estimated the cost of the unguyed poles, the cost of the guyed hardware was removed. The man hour requirements were reduced by 10 hours and the petty contractor cost was reduced by 60 $EC, consistent with the difference seen in the case of the 11 kV guyed vs. unguyed poles.
Benefit-Cost Analysis. In order to examine the potential benefits associated with using Class 1 poles vs. Class 3 and Class 5 poles for the T&D system a benefit-cost analysis was performed. In the analysis discussed in the following, we assume that the system has not yet been built and the cost to upgrade the system represents a cost increase that would have occurred at the planning stage. The benefits associated with the stronger T&D system are the avoided future damages and/or losses. The present value of the benefits, PVB, is expressed as:
Equation 6.8
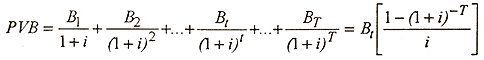
where Bt is the expected annual benefit of a system upgrade, T is the expected useful life of the system, and i is the annual discount rate. The expected useful life of the system is taken as being equal to 60 years, and effective discount rates of 4%, 5% and 6% are examined. Note that the discount rate recommended by the US Federal Emergency Management Agency is 7% and the effective discount rate used by ARA in a similar cost-benefit study performed a U.S. utility was 5.1%. The cost of mitigation is taken as the incremental cost in up-grading from a Class 3 pole to a Class I pole in the case of the 11 kV and 33 kV lines, and the cost of upgrading from a Class 5 pole to a Class 1 pole in the case of the low voltage lines. The benefit cost ratio is simply the ratio of the present value of the benefits to the cost of the up-grade. Benefit-cost ratios greater than unity indicate that the up-grade will pay for itself over its design life.
| Line Type | Pole Cost ($EC) | |
| Class 3 (Class 5 for LV line) | Class 1 | |
| 11 kV Unguyed | 1700 | 2030 |
| 11 kV Guyed | 2200 | 2530 |
| 33 kV Unguyed | 3230 | 3548 |
| 33 kV Guyed | 3623 | 3823 |
| Low Voltage Unguyed | 800 | 1129 |
| Low Voltage Guyed | 1181 | 1511 |
Using the methodology described above, the expected number of poles failed per storm are computed for the 11 kV line, the 33 kV line and the LV lines separately. In the case of the high voltage lines (11 kV and 33 kV) both class 3 and class I poles were examined. In the case of the low voltage lines class 5 and class 1 poles were examined. In the case of the high voltage lines, modeling sensitivity studies for the Class 3 pole cases were performed. In one case the impact of assuming the whole Island could be modeled as open terrain (an extremely conservative assumption) was assessed. In the second case we assumed the island was flat (i.e. speed-up effects were ignored) but the local surface roughness was lefi as in the base case. The expected average annual percentage of failed poles is given as
Equation 6.9
where l is the average annual occurrence rate for storms, and E(n) is the expected number of poles failing per storm. The expected annual percentage of failed tangent poles is given in Table 6.3. Figures 6.2 through 6.4 present the expected fraction of failed poles as a function of the maximum peak gust wind speed (in flat open terrain) simulated at any location on the island. As indicated in Figures 6.2 through 6.4 the expected fraction (or number) of failed poles can vary significantly between storms producing the same maximum peak gust wind speed but at different locations on the island. For example, in the case of the 33 kV line with class 3 poles with a maximum peak gust wind speed of 150 mph, the expected fraction of failed tangent poles ranges between a minimum of about 10% and a maximum of about 46%. This point is mentioned simply to point out that simple extrapolations of damage vs. wind speed can lead to misleading results. Similarly, the comparisons of the damage vs. peak gust wind speeds shown for different terrain types (open country throughout or flat) show that comparisons of damages observed between different Caribbean islands is not advisable.
Figures 6.5 through 6.7 show the expected fraction of failed tangent poles as a function of return period for the various terrain assumptions discussed above.
| Link Type | Description | Annual Percentage of Tangent Poles Failed | |
| Mean | Std. Deviation | ||
| 11 kV | Class 3 Poles, Base Terrain* | 0.6430 | 3.836 |
| 11 kV | Class 3 Poles, Open Country Throughou | 1.059 | 5.709 |
| 11 kV | Class 3 Poles, Flat Terrain | 0.2384 | 1.695 |
| 11 kV | Class 1 Poles, Base Terrain | 0.2138 | 1.759 |
| 33 kV | Class 3 Poles, Base Terrain | 0.7904 | 4.808 |
| 33 kV | Class 3 Poles, Open Country Throughout | 1.814 | 8.599 |
| 33 kV | Class 3 Poles, Flat Terrain | 0.2362 | 2.518 |
| 33 kV | Class 1 Poles, Base Terrain | 0.2547 | 2.255 |
| Low Voltage | Class 5 Poles, Base Terrain | 0.2216 | 1.371 |
| Low Voltage | Class 1 Poles, Base Terrain | 0.01770 | 0.1861 |
*(Base Terrain - Suburban except within 1 km of coast where terrain is open, speed-ups included)
Using the cost data given in Table 6.3, predictions of the average annual losses were computed for the Island. As indicated in Section 3, the failure probabilities computed for the guyed pole structures are too low, and as a result three different assumptions are made regarding the guyed pole failure probabilities. In all three cases we assume that approximately 50% of the poles are guyed, which is consistent with the distribution of line angles as discussed in Section 5 The three guyed pole failure probability assumptions are:
The average annual losses for the above three cases for existing class poles and class 1 poles throughout are given in Table 6.4.
In the opinion of the authors, the expected annual losses of the St. Vincent T&D system is in the range of EC $68,000 to EC $85,000, which represents less than 0.5% of the replacement cost of all poles (conductor costs are not included).
Table 6.5 summarizes the benefit cost ratios for each line examined. The benefits used to develop the benefit-cost ratios given in Table 6.5 are associated with the savings in replacing failed poles and do not include savings due to a reduction in lost sales of benefits associated with reduced insurance premiums.
| Relative Guyed Pole Failure Probability | Line Type | Annual Failure Cost ($EC) | |
| Class 3 and Class 5 | Class 1 | ||
| 1.0 | 11 kV | 79,991 | 32,617 |
| 1.0 | 33 kV | 5,864 | 2,076 |
| 1.0 | Low Voltage | 25,047 | 1,911 |
| 1.0 | Total | 110,902 | 36,604 |
| 0.5 | 11 kV | 65,874 | 26,471 |
| 0.5 | 33 kV | 4,576 | 1,597 |
| 0.5 | Low Voltage | 15,745 | 1,595 |
| 0.5 | Total | 85,195 | 29,663 |
| 0.25 | 11 kV | 52,935 | 21,390 |
| 0.25 | 33 kV | 3,754 | 1,318 |
| 0.25 | Low Voltage | 11,614 | 1,275 |
| 0.25 | Total | 68,303 | 23,983 |
| Line Type | Benefit-Cost Ratio | ||
| Discount Rate=4% | Discount Rate=5% | Discount Rate=6% | |
| 11 kV | 0.46 | 0.39 | 0.33 |
| 33 kV | 1.25 | 1.05 | 0.90 |
| Low Voltage | 0.18 | 0.15 | 0.13 |
The results as presented in Table 6.5 indicate that in the initial design stage, using Class I poles for the low voltage line and/or for the 11 kV line would clearly have been a waste of resources. In the case of the 33 kV line, benefit-cost ratios of greater than one appear for two of the three discount rates examined. The results suggest that the use of Class 1 poles for the 33 kV line would have produced cost savings. The reasons for the higher benefit-cost ratio in the case of the 33 kV line are
The fact that the use of Class 1 poles for the 33 kV line does not mean that the line should be replaced with Class 1 poles (this would not be cost effective), but rather if a benefit-cost analysis had been performed at the design stage, Class 1 poles would probably have been chosen for the 33 kV line. The capacity of the 33 kV line could be increased by using Class 1 poles instead of Class 3 poles in cases where pole replacements are required. The upgrading should be applied to tangent poles only, since increasing the pole size for guyed poles is unlikely to decrease the pole failure probabilities, since guyed pole failures are generally caused by guy connection failures, not pole failures. Using this approach, over time most of the 33 kV line would be comprised of Class 1 poles with the incremental costs being consistent with those used to derive the benefit-cost ratios given in Table 6.5.
The failure costs included in the benefit-cost estimates described above include only the cost of replacing the downed poles. In the following discussion estimates of additional failure costs associated with lost revenue are examined. The assumptions made in this cost analysis are:
Using the assumptions outlined above, the expected annual losses associated with lost revenues produced by failure of the 11 kV line are EC $61,764 and EC $23,949 for Class 3 and Class 1 construction respectively. The benefit-cost ratios (including the cost of rebuilding the 11 kV line) for the three discount rates used are given in Table 6.6. The expected annual lost revenue for the case where 50% of the poles are guyed (with a failure probability of 0.5 times the tangent pole failure probability) are EC $49,150 and EC $19,061 for Class 3 and Class 1 poles, respectively. If the guy pole failure probability is assumed to be 25% of the tangent pole failure probability, then the expected average annual losses associated with lost revenue for the Class 3 and Class 1 pole systems are EC $42,450 and EC $16,539, respectively. The inclusion of lost revenue increases the average annual failure costs by approximately 60% over the replacement cost alone case.
| Discount Ratio | Benefit-Cost Ratio |
| 4% | 0.83 |
| 5% | 0.70 |
| 6% | 0.59 |
The benefit-cost ratios given in Table 6.6 show, that even with the conservative assumptions used to derive the potential lost revenues associated with a hurricane strike, it would not have been beneficial to construct the 11 kV line with Class 1 poles.
Estimates of losses vs. return period are presented in Figures 6.8 and 6.9 for the base case estimates of line failure probability (i.e. assuming the failure probability of the guyed structures is equal to 50% of the tangent structure failure probability). The costs given in Figure 6.8 include replacement costs only, whereas those given in Figure 6.9 include estimates of the lost revenue as well. The estimates of failure cost vs. return period are computed using the same rank ordering approach used to estimate wind speed vs. return period as described in Section 2 of the report. As indicated in Figure 6.9, the estimated mean value of the 100 year (1% annual probability) failure cost of the existing system is about EC $2.3 Million, representing about 10% of the value of the system. The 100 year return period failure cost an upgraded system is about EC $0.8 Million, representing about 3% of the value of the system. If estimates of lost revenue are included in the failure cost estimates then the 100 year return period failure costs for the two systems described above increase to about EC$3.9 Million and EC$ 1.3 Million, respectively.
The study of the St. Vincent T&D system described herein is believed to be the first comprehensive study examining the reliability and potential vulnerability of electric power systems to hurricanes in the Caribbean. The methodology used in the study is based on a probabilistic hazard-vulnerability financial analysis. The windfield and boundary layer models include the effects of topography and terrain on the local surface winds produced by hurricanes. The estimates of wind loads used in the study take into account the turbulent characteristics of the wind and the lack of correlation of the gust portion of the wind over the structures. The effect of wind direction and effects of wind speed up on the flow are also treated. The results show that ignoring the effects of topography can lead to underestimates of the annual failure probabilities by up to a factor of three. Similarly, not taking into account decreases in surface level wind speeds produced by trees, can lead to overestimates of the failure pr6babilities by factors near two. The wind load and response models take into account the increases in the bending moments within the supporting wood poles associated with P-delta effects and foundation flexibility. Increased wind loads produced by transformers located on the poles are included when transformers are present. The resistance of the poles includes a model that takes into account the reduction in capacity of the poles with increasing age. The study includes a separate analysis of guyed poles, where it was found that more research is needed into the guyed pole failure mechanisms and the overall reliability of the guy connections.
The large range in the number of poles failed on the island, given the occurrence of a maximum peak gust somewhere on the island, combined with the significant effects of terrain and topography indicate that comparisons of the number of poles failed on any one island in any one storm should under no circumstances be used to infer the number of poles which might fail on another island in a "similar" storm. The expected number of failed poles is strongly affected by wind direction, storm size, pole distribution over the island, topography and surface roughness.
Within the limitations of the failure modes examined, the results of the benefit-cost analysis indicate that, with the exception of the 33 kV transmission line, the T&D system designed and in use on the island of St. Vincent is more than adequate. One of the reasons for the success of the St. Vincent system is believed to be the lack of communication cables attached to the poles, the existence of which was assumed in the original system design. Considering the long spans and the remote location of much of the 33 kV line, the results of the benefit-cost analysis indicate that the this portion of the system should have been constructed using 45 foot Class I Southern Yellow Pine poles.
The failure modes considered in the analysis herein consider only bending failures. While the soil is treated as an elastic foundation, we did not have sufficient information to develop a soil failure model. The elastic spring approach used to model the soil conditions could be extended to incorporate permanent set or complete failure if adequate soil information is provided. The omission of the a soil failure model would not change the conclusion of the benefit-cost analysis that neither the 11 kV line or the low voltage line poles should be upgraded, although an underestimate of the expected annual number of failed poles could result. Note also we assume that the connections between the conductors and the supporting poles will not fail before the poles fail. If the these connections are under designed then again, the benefit-cost conclusions pertaining to the 11 kV line and the low voltage line are unchanged, but an over estimate of the annual number of failed poles will result. Note that the influence line approach used in this study can be readily extended to include other failure modes, currently not included in the model provided resistance information is available. The impact of the more resilient system on the possibility of obtaining reduced insurance premiums was not included in the benefit-cost study and requires further consideration. Note that for upgrading of poles we consider only increasing the class of wood poles. We did not examine the use of steel poles because we have no information on the increased shipping costs (heavier poles) or information on the impact of these poles on maintenance costs including corrosion protection, etc.
The failure model used in the study has the ability to pin point regions on the island where the risk of failure of the system is higher than average, however, because of cost and time limitations, we are unable to perform this analysis at the present time.
We believe that to properly solve the problem of estimating the losses to the T&D systems and developing cost effective mitigation measures will require a well-focused multi-year program. This program will require detailed post storm field surveys carried out to identify failure modes not included in this study and to validate the model with respect to the failure modes currently modeled. The study performed here identified a need for an improved method to analyze the failure probabilities for guyed structures and better information on the soil characteristics for use in foundation failure models. The study also indicates that improvements to the approach would be possible if more detailed information on the actual positions of pole-line type were available. This better data on pole position, etc., will eliminate the need to sample span lengths, line angles, etc., which add some uncertainty to the results. The program needs to evaluate average annual losses and probable maximum losses for multiple island impact scenarios for the support of the development of an insurance pool. The potential long terms payoffs resulting from a more longer term program are more reliable estimates f losses resulting from the inclusion of more failure modes, the identification of islands where systems need upgrading to cost effectively reduce losses, more defensible loss estimates which can be used when approaching external insurance providers quantitatively to support arguments on the appropriate premiums. Some specific recommendations and needed extensions in the work are discussed below.
An important extension to the work described herein is the validation of the approach through comparisons with observed damage. These comparisons could entail gross comparisons of losses caused by Hurricane Luis on the Islands of Antigua and Anguilla, or the damage produced by Hurricane Marilyn in St. Thomas. Both of these storms occurred during 1995 and reasonably good information on the number of failed and tilted poles should be available. Note, that one advantage in using the Anguilla or Antigua data is that the islands are relatively flat and open and thus damage comparisons can be made without introducing significant terrain effects. This allows only the failure model to be tested without introducing additional uncertainties associated with the terrain model(s). If any of the Caribbean Islands experience Hurricane damage during the 1996 Hurricane season, again comparisons to observed damage should be made. If such an event should occur, we recommend that a detailed damage survey be performed where, in addition to determining the total number of failed and tilted poles, the survey should include information on the relative number of guyed pole failures and conductor or conductor connection failures. This type of damage survey would include two persons in the field for sufficient time to collect the detailed failure mode data which is needed to supplement the damage data obtained by the affected utility. This failure mode data would then be used in conjunction with a simulation of the storm to produce estimates of the wind speeds experienced by the structures during the event.
Once further data is obtained to calibrate the model used in this study and to identify other failure modes, the approach can be readily extended to other islands. The identification of other failure mechanisms and the overall validation of the methodology used in this study probably will not have a significant impact on the conclusions drawn from the benefit-cost analyses, but will be of more importance in assessing insurance premiums and estimating the optimum reserves if self insurance is considered.
Abramowitz, M., and I.A. Stegun (Eds.), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover Publications, New York, 1972.
Davenport, E.G., "Gust Response Factors for Transmission Line Loading," Proceedings 5th International Conference on Wind Engineering, (J.E. Cermack, Ed.), Pergamon Press, New York, NY, Vol.2, pp.899-909.
Engineering Sciences Data Unit, Characteristics of Atmospheric Turbulence Near the Ground.
I. Definitions and General Information, Data Item Number 74030, London, England, 1974.
Engineering Sciences Data Unit, Characteristics of Atmospheric Turbulence Near the Ground II: Single Point Data for Strong Winds (Neutral Atmosphere), Data Item Number 85020, London, England, 1985.
Engineering Sciences Data Unit, Characteristics of Atmospheric Turbulence Near the Ground.
III: Variations in Space and Time for Strong Winds (Neutral Atmosphere), Data Item Number 86010, London, England, 1986.
Goodman, J.R., and A.H. Stewart, "Wood Pole Management - Utility Case Studies," IEEE Transactions on Power Delivery, Vol.5, No.1, January 1989.
Lemelin, D.R., "A Study of Wind Speed-Ups and Wind Loading of Buildings in Complex Terrain," Master of Engineering Science, University of Western Ontario, London, Ontario, September 1987.
Vickery, P.J., and L.A. Twisdale, "Prediction of Hurricane Windspeeds in the U.S.," Journal of Structural Engineering, Vol.121, No.11, November 1995a.
Vickery, P.J., and L.A. Twisdale, "Wind-Field and Filling Models for Hurricane Wind-Speed Predictions," Journal of Structural Engineering, Vol. 121, No.11, November 1995b.
Wind loads acting on electric power transmission and distribution systems are comprised of both mean and dynamic components. In general, the dynamic component of the response of a structure to the turbulent action of wind is comprised of a quasi-static (or background turbulence) component and a resonant component. Following the assumption used in ASCE Manual of Practice Number 74 for estimating wind loads on transmission systems, the resonant component of the dynamic response is neglected in this study.
The mean drag response, R-bar, of any structure subjected to wind loads is computed from
Equation A.1
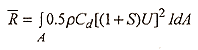
where, Cd is a drag coefficient, U is the mean wind speed in flat terrain, S is a topographic wind speed-up factor, I is an influence coefficient converting the wind load at a given point to a response (e.g. bending moment, deflection, etc.), r is the density of air, dA is an incremental area, and A is the frontal area of the structure. For an electric power transmission or distribution system the frontal area includes the support structure and one complete span length.
The variance of the background response, s2r of the structure to the turbulent wind is computed from
Equation A.2
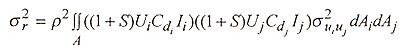
where the sub-scripts i and j represent two separate points on the structure and s2uiuj is the covariance of the fluctuating horizontal component of turbulence at locations i and j. The double integral is evaluated over the entire frontal area of the structure.
The peak response of the structures, R-hat, computed from
Equation A.3
where g is a peak factor, typically taking on a value between 3 and 4. A value of 3.75 is used for the peak factor here. Provided information on the turbulent characteristics of the wind and the necessary drag coefficients, influence coefficients, etc. are known, Equations (A.1) through (A.3) can be used to predict the response of any drag sensitive structure to wind loads, if the resonant component of the response can be neglected. As indicated in Equations A.1 and A.2, in instances where wind speed-up is modeled, only the mean component of the wind speed is increased and the standard deviation of the longitunal velocity fluctuations, su, is left unchanged.
The modeling 6f the turbulent structure of the hurricane boundary layer for use in the calculation of wind loads acting on the distribution system used herein is based on the premise that near the ground, the overall characteristics of the flow are governed by the local surface roughness. With this assumption, boundary layer models developed for large scale storm Systems can be used to describe the flow characteristics near the ground. The boundary layer models used are based on the Engineering Sciences Data Unit (ESDU) models developed over the past two decades.
For a homogeneous terrain the mean velocity, U, at height z is obtained from
Equation A.4
U = 2.5u*ln(z/z0)
where u* is the friction velocity and z0 is the surface roughness length.
The turbulence intensity at height z above ground, Iu, given as
Equation A.5
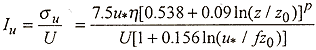
where
h = 1-6fz/u* ; p=h16
where f is the coriolis parameter and su is the rms longitudinal velocity. The peak gust wind speed at height z, � is obtained from
Equation A.6
where the peak factor, g is assigned a value of 3.5.
The co-variance, s2uiuj, is obtained from
Equation A.7
where the cross-correlation coefficient is given as
Equation A.8
and
Equation A.9
where Dr is the distance between points i and j, and rLu is the compound turbulence length scale defined as
Equation A.10
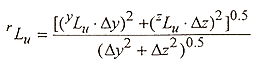
where Dy and Dz are the distances between points i and j. Note that the y direction is perpendicular to the direction of the mean wind and z is the height above ground. The principal turbulent length scales are given as
Equation A.11
Equation A.12
where z0 is the local surface roughness.
Equations (A.4) through (A.12) are used in conjunction with equations (A.1) through (A.3) to obtain estimates of the peak wind load effects on the distribution system structures. In the investigation described herein, two values of surface roughness are used to model the Island, namely 0.03 meters for open terrain, and 0.3 meters for suburban of forested terrain.
Guyed utility pole stresses are computed with the aid of influence matrices computed using the stiffness method (or displacement method). The stiffness method is developed on the basis of writing joint equilibrium equations in terms of stiffness coefficients and unknown joint displacements. The method has been established for many years and its development can be found in most advanced structural analysis texts.
The model used to represent the guyed utility pole is shown in Figure B. 1. The model consists 52 elements with a total of 158 degrees of freedom. A roller is placed at the base of the pole so that rotation and horizontal motion within the soil is possible. The stiffness provided by soil and guy wires is modeled using discrete springs and is taken into account by adding the stiffness terms to the appropriate diagonal elements of the global stiffness matrix.
The stiffness used for soil is based on an average of representative values of lateral
modulus of sub-grade reaction, ks, for medium wet clay and medium
saturated clay. Discrete spring constants, ![]() ,at a depth i are
computed as:
,at a depth i are
computed as:
Equation B.1
where Ai is the projected frontal area of the submerged pole at a depth i. A total of 13 discrete "soil" springs are used to model the stiffness provided by the six feet of soil.
The stiffness of the springs representing the guy wires, located at the attachment points of guy and utility pole, are given by
Equation B.2
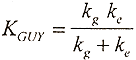
where kg is the geometric stiffness term
Equation B.3
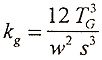
where
Equation B.4
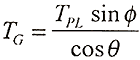
and where w is the guy linear weight. Terms F, q, and TPL are defined in Figure B.2. The elastic stiffness term, ke, is given by
Equation B.5
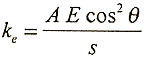
where A and E are guy wire cross sectional area and modulus of elasticity, respectively.
A base moment influence diagram is shown in Figure B.3 for a 45 ft guyed utility pole. Figure B.4 shows the bending moment diagram for the same utility pole subject to uniform wind loading. The effect of guy stiffness on base bending moment is shown in Figure B.5 for the same uniform pressure loading. As the guy stiffness increases base bending moments are significantly reduced. It should be noted that in the development of the guy stiffness values, we assume that the guys are properly pre-tensioned to balance the horizontal forces exerted by the tension in the conductors, and deviations in the guy pre-stress will change the distribution of the bending moments in the utility pole. In Figure B.5, the inner most bending moment diagram, corresponds to that which would exist if the guys were properly pre-stressed. The outer most bending moment diagram corresponds to the case of a free standing utility pole.
Tables B. 1 and B.2 present the material properties used to model utility poles and guy wires.
| Material | Modulus |
| Southern Yellow Pile | 2.51 x 106 psi |
| Wire Type | Effective Area | Modulus | Weight |
| 7/16" | 0.1488 in2 | 2.7 x 107 psi | 0.4 lb ft 1 |
In order to compute bending moments and guy forces as a function of wind speed, influence coefficients were developed for the bending moment at the base each segment of the pole and for the guy forces. Using the methodology outlined in Section 3.1, the mean, RMS and peak bending moments and guy forces were computed for each wind speed examined. Failure was considered to occur if the peak bending stress (plus any initial compressive stresses due to guy pre-tension) at any location on the pole exceeded the modulus of rupture, of if the guy forces exceeded the ultimate capacity of the guy wire. We obtained information on the ultimate capacity of a 7/16 inch high strength steel guy wire from a local supplier. The ultimate load provided to us was 60,000 pounds which included a factor of safety of 3. Using the guy capacity data combined with the pole strength data discussed earlier, we found that the probability of a properly guyed pole failing in hurricane force winds was extremely low. The overestimate of the capacity of the guyed poles is thought to be a result of not modeling the connections in the guy system and not modeling errors in the initial pre-tensioning of the guys. The observation that guyed poles do fail, and that failure is typically initiated in the guy system indicates our model is not taking into account all possible failure mechanisms.
| CDMP home page: http://www.oas.org/en/cdmp/ | Project Contacts | Page Last Updated: 20 April 2001 |