Caribbean Disaster
Mitigation Project
Implemented by the Organization of American States
Unit of Sustainable Development and Environment
for the USAID Office of Foreign Disaster Assistance and the Caribbean Regional Program
Caribbean Disaster
Mitigation Project |
Note: This paper was originally published in the 10th Symposium on Global Change Studies, 10-15 Jan 1999. Dallas, TX, by the AMS, Boston MA.
Mark E. Johnson* and Charles C.
Watson, Jr.
University of Central Florida, Orlando, FL; Watson Technical Consulting, Inc., Rincon, GA
Return periods capture the essence of uncertainty in extreme meteorological phenomena (storm surge, wave, and wind) associated with hurricanes. Unfortunately, a detailed historical record of hurricane activity in the Atlantic Basin is only slightly more than one hundred years, making return period estimation of "storm-of-the-century" effects problematic. The purpose of this paper is to describe statistical methodology to address the problem of return period estimation. Initially conceived in a project for the Organization of American States (Montego Bay, Jamaica), the methodology was subsequently refined and expanded in the context of various consulting projects and a large contract with the Division of Community Affairs for the state of Florida involving hazard mitigation. Output from our work includes both maximum likelihood estimates of extremes and their associated uncertainties. Hence, our approach can provide rational assessments of the uncertainty that is more technically sophisticated than the commonplace but extremely conservative method of inflating the Saffir-Simpson category.
In addition to outlining the methodology, the presentation will demonstrate applications to the full North Atlantic basin with GIS-based output products and extensive validation/verification tests. An additional benefit of the approach is that it affords us the opportunity to assess directly the impacts of El Nino and la Nina by partitioning the historical hurricane record appropriately. Other phenomena outside the Atlantic Basin presumed to impact hurricane frequency and intensity are characterized according to their impacts on the return period estimates and corresponding uncertainty. Overall, the methodology offers a sounder statistical basis than the conventional scan radius method.
The statistical methodology for return period estimation and attendant confidence and prediction limits has been detailed by Johnson and Watson (1998). We summarize the basic steps in this section. Following Simiu and Scanlan (1996), return period is defined as the reciprocal of the probability of observing a specific hurricane effect (or more extreme effect) in a single year. The method used at an individual site for a single phenomena (wind, wave or storm surge) is applied at every site in a study region. Hence, it suffices to explain the methodology for the generic situation in which we have 112 years (1886-1997) of annual maxima at a site, say x1, x2, …, x112. The steps are given, as follows:
n/b - n ln b S ln xi - S (xi /b )a ln (xi /b ) = 0, where
b
= [( S xia ) / n] 1/a .x1-p = [- b ln(1 – p)] 1/a ,
where the parameters represent the computed MLEs.
¶
2 ln L / ¶ a ¶ a = - n/a 2 - S (xi /b )a [ln (xi /b )]2¶
2 ln L / ¶ a ¶ b = - n/b + (a /b ) S (xi /b )a ln (xi /b ) + (1/b ) S (xi /b )a¶
2 ln L / ¶ b ¶ b = (na /b 2) { 1 - [(a +1)/(nb a )] S xia }where ln L is the logarithm of the likelihood function and all summations proceed from i equal one to n (n equals 112 if the full HURDAT data set is being used).
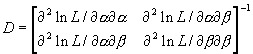
s 1 = Ö D11
s
2 = Ö D22r
= D12 / (Ö D11Ö D22 )where Dij is the (i, j)th element of the matrix D.
- Generate independent normal variates X and Y and a uniform variate U.
- Compute
V = s 1 X + a
W = s 1 [r X + Ö (1-r 2) Y] + b
R = W [- ln (1 – U1/n )] 1/V,
where a and b are the MLEs. Repeat this simulation process a large number, say N times (1000 should suffice for up to 99% prediction limits), storing the generated R values. Sort them in ascending order and the (0.90 x N)th item is the simulated 90% prediction limit.
Further details on implementation of the above steps can be found in Johnson and Watson (1998).
To illustrate the methodology of Section 1, consider the location Belize City, Belize. Figure 1 provides a plot of the fitted Weibull distribution overlayed with a histogram of the annual maximum winds.
Of greater interest may be basin wide results. Figure 2 gives upper 90% prediction limits for 50 year return period winds. Additional applications of the return period methodology can be found in Johnson and Watson (1998).
Johnson, M. E., 1997: Caribbean Storm Surge Return Periods, Organization of American States Caribbean Disaster Mitigation Project Workshop, Kingston, Jamaica, October 31, 1997.
Johnson, M. E. and Watson, C. C., Jr., 1998: Return Period Estimation of Hurricane Phenomena, submitted.
Neumann, C. J., Jarvinen, B. R., McAdie, C. J., and Elms, J. D., 1993: Tropical Cyclones of the Atlantic Ocean, 1871-1992, Asheville: National Climatic Center Data Center.
Simiu, E. and Scanlan, R. H., 1996: Wind Effects on Structures. New York: Wiley.
Watson, C. C., Jr., 1995: The Arbiter of Storms: A High Resolution, GIS-based System for Integrated Storm Hazard Modeling, National Weather Digest, 20, 2-9.
Watson, C. C., Jr., 1997: TAOS Model for the Caribbean, Organization of American States Caribbean Disaster Mitigation Project Workshop, Kingston, Jamaica, October 31, 1997.
* Corresponding author address: Mark E. Johnson, Univ. of Central Florida, Dept. of Statistics, Orlando, FL 32816-2370; e-mail: [email protected]
| CDMP home page: http://www.oas.org/en/cdmp/ | Project Contacts | Page Last Updated: 20 April 2001 |